Escrito por Ramón Saquete
Lo prometido es deuda, así que aquí tenéis la segunda parte de cómo funciona un buscador o Information Retrieval System (IRS). En la primera parte aprendimos como se construye el índice inverso, que nos dice qué documentos tiene asociados cada palabra y qué importancia o relevancia tienen las palabras en cada uno de ellos. En esta segunda parte veremos cómo se utiliza ese índice para devolver los documentos, ordenados por relevancia, dada una consulta del usuario.
Para realizar esta tarea, primero vamos a pre-procesar la consulta tal y como se hizo en la indexación, es decir, si en la indexación se eliminaron stop words y se calculó la raíz de las palabras, en la consulta haremos lo mismo. Después calcularemos el peso de cada término o keyword de la consulta con una fórmula que puede ser parecida a la siguiente:
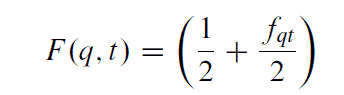
De esta forma cada palabra de la consulta tiene asociado un valor numérico. Estos valores numéricos sirven para representar la consulta como un vector dentro de un espacio n-dimensional donde cada dimensión es una palabra distinta, veámoslo con un ejemplo:
Supongamos que el usuario introduce la siguiente consulta: «Human Level». Esta consulta está formada por dos palabras y según la fórmula anterior estos serían sus pesos:
F(q,Human) =0,5+0,5=1
F(q,Level)=0,5+1=1,5
Como son sólo dos palabras distintas, podemos representarlas en una gráfica de dos dimensiones en donde, por ejemplo, Human sería el eje X y Level el eje Y:
Ahora es cuando entra en juego el índice inverso, que nos dice en qué documentos aparecen esas dos palabras y además qué peso tienen en éstos. Con esta información ahora podemos representar cada documento dentro del espacio vectorial anterior, junto a la consulta. Vamos a suponer que en el índice tenemos los siguientes valores:
Formato del índice: Término --> Documento, peso | Documento, peso | ... Human --> 1,2 | 2,1 | 3,4 Level --> 2,1 | 3,3 | 4,2
Con esta información sabemos que tenemos los siguientes vectores para cada documento:
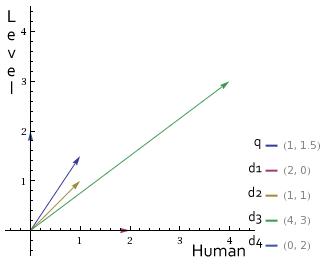
Dimensión X (Human), Dimensión Y (Level) Documento 1 =(2 , 0 ) Documento 2 =(1 , 1 ) Documento 3 =(4 , 3 ) Documento 4 =(0 , 2 )
Ahora ya podemos representarlos gráficamente junto al vector de la consulta:
Los vectores de los documentos en los que importe más la palabra Level estarán más cerca del eje Y, los vectores de los documentos en los que tenga más relevancia la palabra Human estarán más cerca del eje X y en la diagonal las dos palabras serán igual de relevantes.
Para entender bien una fórmula siempre es más fácil visualizar lo que hace y esta representación gráfica, como es lógico, no la hace internamente el IRS, simplemente es para que comprendáis ahora el significado geométrico del cálculo de la relevancia.
Nos hemos ido de la representación textual de la que partíamos a una representación con vectores en un espacio euclídeo sobre la que podemos aplicar fórmulas del campo del álgebra lineal. Lo que vamos a hacer a continuación es aplicar una fórmula para medir las distancias que hay entre el vector de la consulta y todos los vectores de los documentos. Estas distancias nos van a decir en cuánto se asemeja cada documento a la consulta y, por lo tanto, va a ser nuestra medida de relevancia para mostrar finalmente al usuario los documentos ordenados.
Hay muchas formas de calcular esta distancia, pero la más popular en los IRS es la distancia del coseno:
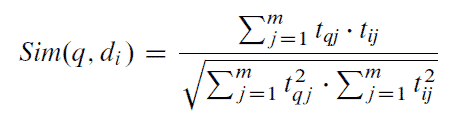
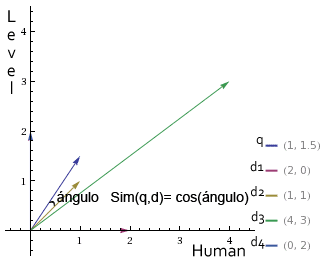
Quizás os habréis fijado que en la fórmula de la distancia del coseno, aparentemente no aparece ningún coseno, esto es porque la medida de similitud que devuelve esta fórmula, es en realidad, el coseno del ángulo que forman los dos vectores. Ver imagen:
Explicaré esto más detalladamente en los dos siguientes párrafos, para aquellos que les interese la explicación matemática:
En el numerador estamos sumando el peso de cada término en la consulta multiplicado por el peso que tiene ese mismo término en el documento. Los más avispados, ya se habrán dado cuenta de que en realidad lo que estamos haciendo aquí, es calcular el producto escalar o producto punto, entre el vector de la consulta y el documento. Sabiendo que el producto escalar también se puede calcular de la siguiente forma:
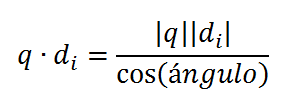
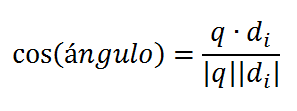
Finalmente, tenemos un valor de relevancia entre 0 y 1 para cada documento que nos permite ordenarlos:
Sim(q,d2)=0,9976 < Documento más relevante
Sim(q,d3)=0,9778
Sim(q,d4)=0,7546
Sim(q,d1)=0,6562 < Documento menos relevante
Aunque lo cierto es que la relación entre la distancia del ángulo y la relevancia real, es en realidad un poco vaga, por lo que esta fórmula nunca se utiliza tal cual, sino que es modificada y reforzada con bastante información adicional. En este sentido, sabemos muchos de los factores on-page y off-page que utiliza Google como el PageRank, la geolocalización y el idioma de la consulta, tu historial de búsquedas, la actividad en redes sociales, etc.
Para ofrecer resultados más ricos, además se puede expandir la consulta del usuario con sinónimos, conjugaciones, plurales o palabras relacionadas o, si no se expande, también se pueden incluir los resultados de variaciones de la consulta.
Para todo lo anterior, no sólo se utilizan fórmulas matemáticas y estadísticas sino innumerables técnicas de inteligencia artificial como lógica difusa, redes neuronales, algoritmos genéticos, clasificadores bayesianos, support vector machines, algoritmos de grafos, etc.
Por otro lado, los buscadores cada vez más, incorporan respuestas de otro tipo de sistemas más inteligentes, los Question Answering Systems. Estos sistemas, al contrario que los IRS, lo que hacen es devolver respuestas concretas a las preguntas que introducen los usuarios, funcionalidad que se ve potenciada por el crecimiento de la Web semántica. Podemos ver un ejemplo introduciendo en Google la siguiente pregunta:
¿Cuánto mide la torre Eiffel?
En definitiva, los buscadores son inteligencias artificiales capaces de aprender, evolucionar y reajustarse a sí mismas continuamente, provocando que ni los propios ingenieros que las programan y las mantienen, puedan llegar a comprender por completo su funcionamiento. Por eso y porque las SERPs ahora se ajustan a cada usuario, los consultores SEO honestos, como los de Human Level, nunca te asegurarán que puedas conseguir la primera posición para una determinada palabra, sino que pueden hacer que tus páginas aumenten posiciones y consigan más tráfico.